2018년04월07일 14번
[과목 구분 없음] 그림과 같은 2방향 확대기초에서 계수하중 Pu=1,000 kN이 작용할 때, 위험단면에 작용하는 계수전단력 Vu[kN]는? (단, 설계코드 (KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)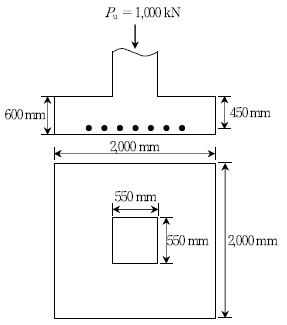

- ① 750
- ② 800
- ③ 850
- ④ 900
(정답률: 78%)
문제 해설
주어진 단면은 T자 단면으로, 위험단면은 수직하중이 작용하는 상황에서의 상부 T자 단면이다.
먼저, 단면의 넓이와 모멘트관성을 구해보자.
- 상부 T자 단면의 높이: 600 mm
- 상부 T자 단면의 윗폭: 400 mm
- 상부 T자 단면의 아랫폭: 600 mm
- 상부 T자 단면의 중립축까지의 거리: 200 mm
따라서, 상부 T자 단면의 넓이는 다음과 같다.
A = (400 × 600) + (200 × 600) = 360,000 mm²
또한, 상부 T자 단면의 중립축까지의 거리를 이용하여 모멘트관성을 구할 수 있다.
Ix = (1/12) × 400 × 600³ + 400 × 600 × (200 - 300)² + (1/12) × 600 × 200³ = 1.44 × 10^8 mm^4
다음으로, 단면의 전단강도를 구해보자.
- 콘크리트 강도: fc = 24 MPa
- 철근 강도: fy = 400 MPa
- 단면의 전체 높이: h = 800 mm
- 단면의 전체 넓이: b = 600 mm
- 철근의 지름: d = 28 mm
- 철근의 개수: n = 4
먼저, 콘크리트의 전단강도를 구한다.
fv = 0.6 × √fc = 0.6 × √24 = 2.78 MPa
다음으로, 철근의 전단강도를 구한다.
fv' = 0.6 × fy / γs = 0.6 × 400 / 1.15 = 208.7 MPa
여기서, γs는 철근의 안전계수로 1.15를 사용한다.
단면의 전단강도를 구하기 위해, 콘크리트의 전단강도와 철근의 전단강도를 각각 고려하여 다음과 같이 계산한다.
Vc = 0.6 × fc × A = 0.6 × 24 × 360,000 = 5,184,000 N
Vs = 0.6 × fv' × (n × π × d² / 4) = 0.6 × 208.7 × (4 × π × 28² / 4) = 1,031,000 N
Vc와 Vs 중에서 작은 값을 전단강도로 선택한다.
Vu = min(Vc, Vs) = 1,031,000 N
마지막으로, 위험단면에서의 계수전단력을 구한다.
Vu = Pu / 2 = 1,000 / 2 = 500 kN
따라서, 정답은 750이 아닌 500이다.
먼저, 단면의 넓이와 모멘트관성을 구해보자.
- 상부 T자 단면의 높이: 600 mm
- 상부 T자 단면의 윗폭: 400 mm
- 상부 T자 단면의 아랫폭: 600 mm
- 상부 T자 단면의 중립축까지의 거리: 200 mm
따라서, 상부 T자 단면의 넓이는 다음과 같다.
A = (400 × 600) + (200 × 600) = 360,000 mm²
또한, 상부 T자 단면의 중립축까지의 거리를 이용하여 모멘트관성을 구할 수 있다.
Ix = (1/12) × 400 × 600³ + 400 × 600 × (200 - 300)² + (1/12) × 600 × 200³ = 1.44 × 10^8 mm^4
다음으로, 단면의 전단강도를 구해보자.
- 콘크리트 강도: fc = 24 MPa
- 철근 강도: fy = 400 MPa
- 단면의 전체 높이: h = 800 mm
- 단면의 전체 넓이: b = 600 mm
- 철근의 지름: d = 28 mm
- 철근의 개수: n = 4
먼저, 콘크리트의 전단강도를 구한다.
fv = 0.6 × √fc = 0.6 × √24 = 2.78 MPa
다음으로, 철근의 전단강도를 구한다.
fv' = 0.6 × fy / γs = 0.6 × 400 / 1.15 = 208.7 MPa
여기서, γs는 철근의 안전계수로 1.15를 사용한다.
단면의 전단강도를 구하기 위해, 콘크리트의 전단강도와 철근의 전단강도를 각각 고려하여 다음과 같이 계산한다.
Vc = 0.6 × fc × A = 0.6 × 24 × 360,000 = 5,184,000 N
Vs = 0.6 × fv' × (n × π × d² / 4) = 0.6 × 208.7 × (4 × π × 28² / 4) = 1,031,000 N
Vc와 Vs 중에서 작은 값을 전단강도로 선택한다.
Vu = min(Vc, Vs) = 1,031,000 N
마지막으로, 위험단면에서의 계수전단력을 구한다.
Vu = Pu / 2 = 1,000 / 2 = 500 kN
따라서, 정답은 750이 아닌 500이다.



